Introduction:
In the realm of drug development, the pursuit of safe and effective medications is an unwavering goal. To achieve this, exposure-response analysis stands as a vital tool, unlocking the profound relationship between drug exposure and its therapeutic and adverse effects. In this persuasive blog post, we’ll delve into the undeniable importance of exposure-response analysis in drug development, exploring its transformative potential with the inclusion of key equations for exposure-response models. Prepare to be amazed!
Unveiling the Equation-Driven Insights:
Exposure-response analysis encompasses a range of mathematical models and statistical equations that unravel the intricate connection between drug exposure and patient response. By harnessing these equations, researchers can gain invaluable insights into drug efficacy and safety. Let’s delve into a few of these equations and their significance:
Emax Model:
The Emax model is a powerful equation that captures the relationship between drug concentration (C) and the maximum effect (Emax) achievable by the drug. This equation takes the form: E = Emax * C / (C + EC50)
Here, E represents the observed effect, Emax denotes the maximum effect achievable, C signifies the drug concentration, and EC50 stands for the concentration at which 50% of the maximum effect is achieved.
The Emax model provides a robust framework for quantifying the impact of drug exposure on therapeutic outcomes, allowing researchers to optimize dosing regimens for maximum efficacy.
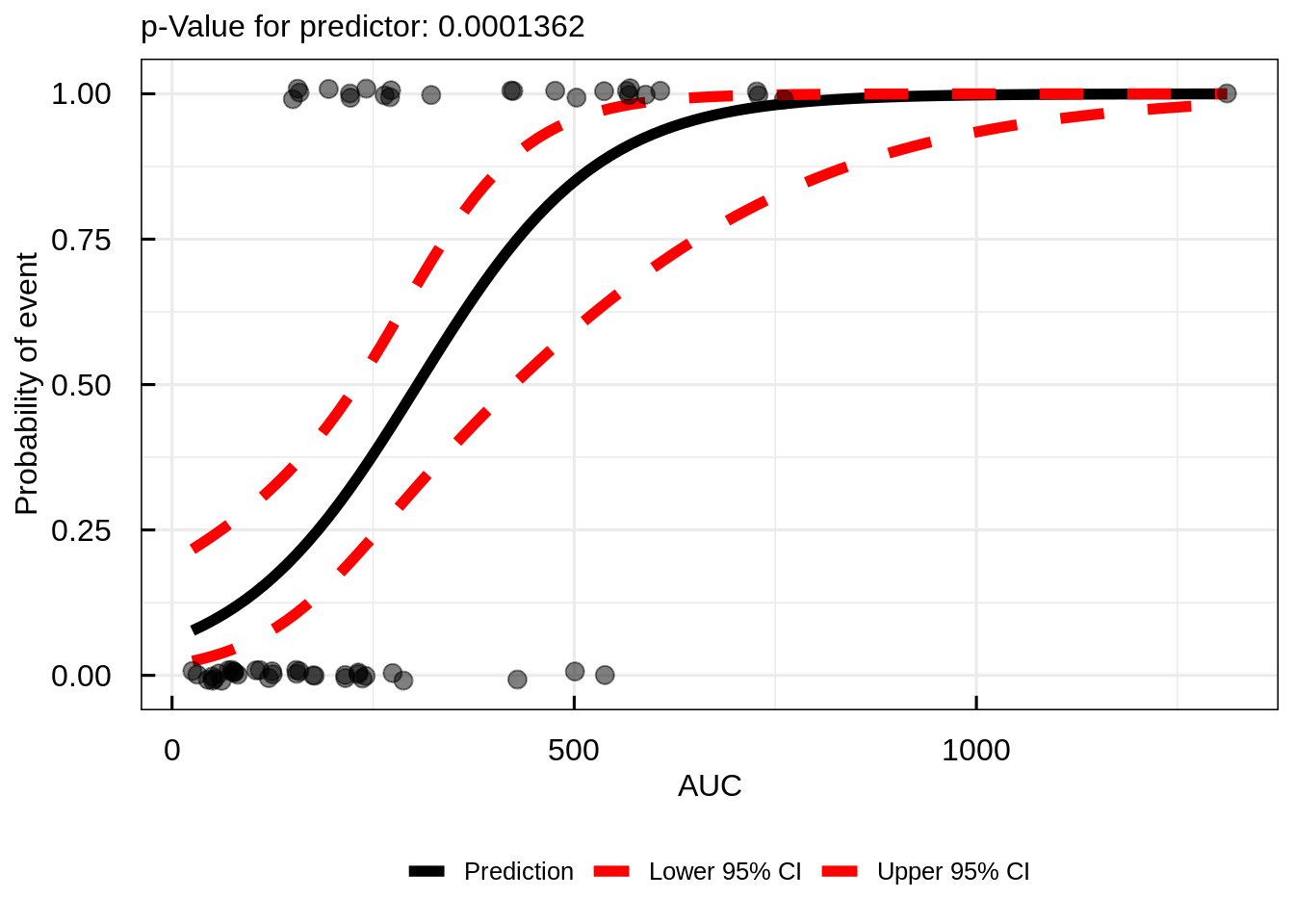
Logistic Regression Model:
The logistic regression model plays a pivotal role in predicting binary outcomes, such as the occurrence of adverse events, based on drug exposure. The equation takes the form: P = e^(β0 + β1 * C) / (1 + e^(β0 + β1 * C))
Here, P represents the probability of a binary response, β0 and β1 are regression coefficients, and C signifies the drug concentration.
Through logistic regression modeling, researchers can quantify the relationship between drug exposure and the probability of specific outcomes, enabling them to mitigate potential risks and enhance patient safety.
Linear Pharmacokinetics:
Linear pharmacokinetic equations describe the concentration-time profiles of drugs within the body. One such equation is: C = D / V * e^(-k * t)
Here, C represents the drug concentration at time t, D signifies the drug dose, V denotes the volume of distribution, k stands for the elimination rate constant, and e represents the base of the natural logarithm.
Linear pharmacokinetics facilitates a comprehensive understanding of how drug concentrations change over time, enabling researchers to optimize dosing strategies and ensure effective therapeutic outcomes.
Transforming Drug Development:
Equipped with exposure-response models and their accompanying equations, researchers can revolutionize drug development. Here’s how exposure-response analysis impacts various aspects of the process:
Optimizing Efficacy:
By utilizing exposure-response models, researchers can identify the optimal drug concentrations required to achieve desired therapeutic effects. These equations enable precise dosing regimens, ensuring patients receive the right amount of medication for maximum benefit. Tailoring treatments to specific patient populations becomes possible, enhancing efficacy across diverse groups. Enhancing Safety Profiles: Exposure-response analysis aids in understanding the relationship between drug exposure and adverse events. By utilizing equations, researchers can determine exposure thresholds beyond which the risk of side effects significantly increases. This knowledge helps establish safe dosing limits and design risk mitigation strategies, ultimately prioritizing patient safety. Supporting Regulatory Decisions: Regulatory agencies rely on exposure-response analyses to evaluate drug efficacy and safety during the approval process. Equations and models provide robust evidence that influences critical regulatory decisions, including dosing recommendations, labeling guidelines, and risk mitigation strategies. The integration of exposure-response analysis facilitates evidence-based decision-making, enhancing the overall quality of medications.
Conclusion:
Exposure-response analysis, fortified by mathematical equations and statistical models, is an indispensable tool in modern drug development. The inclusion of equations such as the Emax model, logistic regression, and linear pharmacokinetics enables researchers to optimize drug efficacy, enhance safety profiles, and support regulatory decision-making.
With exposure-response analysis at the forefront, pharmaceutical companies can revolutionize the landscape of healthcare, bringing forth safer and more effective medications that transform the lives of patients worldwide. Embrace the power of exposure-response analysis and join the movement towards a brighter, healthier future.