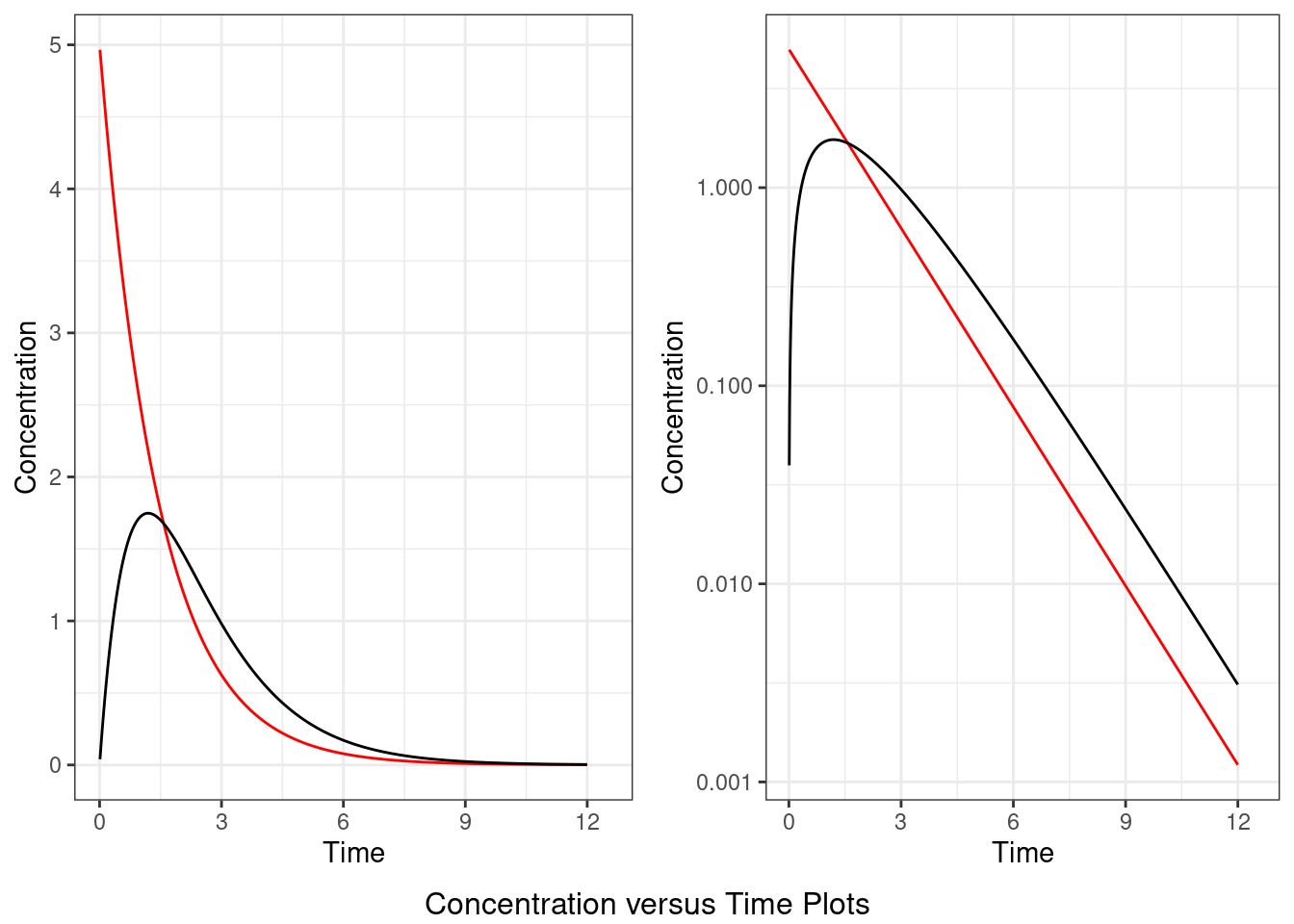
Pharmacokinetics is the study of what the body does to the drug - it is the movement of a drug into, within and out of the body. It describes the relationship between the dose of a drug and its concentration in the body as a function of time. The time course of a drug’s concentration following administration in the body is governed by four processes, which are:
Absorption: uptake of the drug from the administration site into the systemic circulation
Distribution: dispersion of the drug following absorption (if applicable) into the different body organs and tissues
Metabolism: transformation of a drug, usually via specialized enzymatic systems, into compounds that are more readily excreted from the body
Excretion: removal of the drug and metabolites (if applicable) from the body
Collectively, the listed four processes are commonly referred to as ADME.
A basic mathematical equation for pharmacokinetic models is as follows,
\[ C(t) = f_{PK}(dose, t, 𝜃^{PK}) \]
where, \(C\) is the concentration of a drug (commonly in plasma or serum), \(PK\) is pharmacokinetics, \(t\) is time and \(𝜃^{PK}\) is pharmacokinetic parameters that describe the relationship between the dose of a drug and its concentration over time. Pharmacokinetic parameters that are commonly of interest include clearance (\(CL\)), volume of distribution (\(V\)) and the elimination rate constant (\(k_e\) which can be derived by dividing \(CL\) by \(V\)). For extraveneously administered drugs both bioavailability (\(F\)) and the absorption rate constant (\(k_a\)) are parameters that are commonly of interest.
Pharmacodynamics is the study of what the drug does to the body - the drug’s effects. It describes the relationship between drug concentrations and effects. For a drug to exert its effect it typically involves the distribution of the drug from its site of administration to its site of action where it interacts with its target, most typically a receptor, in the body that turns on or off a biochemical or physiological process. The drug effect can be the desired therapeutic effect of the drug, but also may be an undesired adverse effect.
A basic mathematical equation for pharmacodynamic models is as follows,
\[ E(C)=f_{PD}(C, 𝜃^{PD}) \]
where, \(E\) is drug effect, \(C\) is drug concentration, \(PD\) is pharmacodynamics and \(𝜃^{PD}\) is pharmacodynamic parameters that describe the relationship between drug concentrations and effect.
The magnitude of a drug’s effect is dependent on the concentration of a drug. However, the relationship between a drug’s concentration and pharmacodynamic effect is typically non-linear. In other words, this means that doubling the concentration of a drug may not result in a two-fold increase in the drug’s effect. Rather, a drug’s pharmacological effects tend to asymptote to a maximum effect (\(E_{max}\)), resulting in a reduced increase in effect with further increases in concentration.
Warning in scale_x_log10(): log-10 transformation introduced infinite values.
log-10 transformation introduced infinite values.
log-10 transformation introduced infinite values.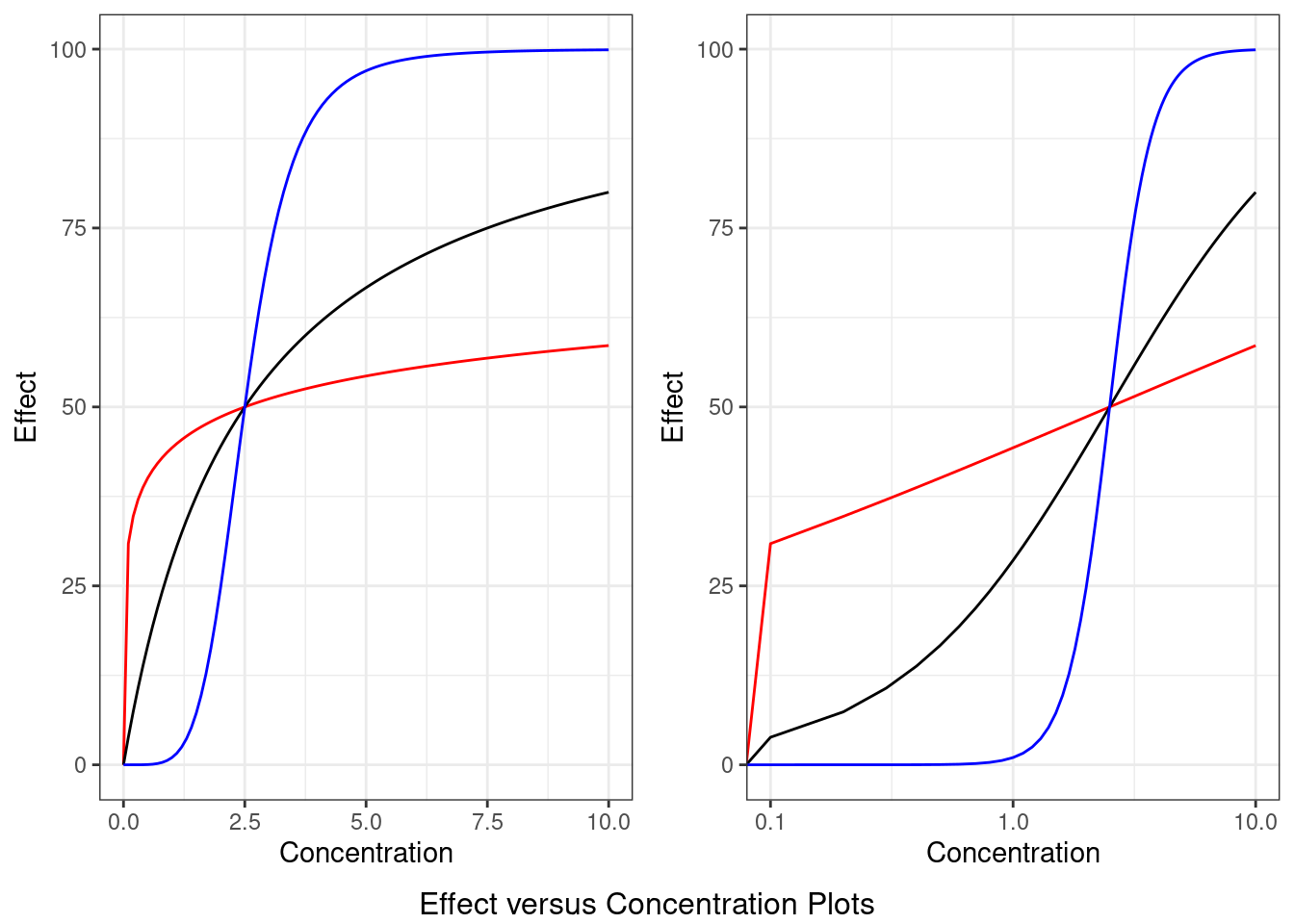
Together, pharmacokinetics-pharmacodynamics, commonly referred to by its abbreviation PKPD, is the study of the time course of the onset and duration of drug effects. A basic mathematical equation for pharmacokinetic-pharmacodynamic models is as follows,
\[ E(t) = f_{PD}(f_{PK}(dose, t, 𝜃^{PK}),𝜃^{PD}) \]
where, the drug effect is now expressed as a function of time dependent on both PK parameters (\(𝜃^{PK}\)) and PD parameters (\(𝜃^{PD}\)). In general, PKPD models are divided into two categories, which are (i) immediate effect PKPD models and (ii) delayed effect PKPD models. The choice of the link used to combine pharmacokinetic and pharmacodynamic data depends on the time relationship between drug exposure and effect.
An immediate effect PKPD model assumes that there is no time delay between a drug’s pharmacokinetics and pharmacodynamics. This means that the drug’s effects follows the same time course as the drug’s exposure (e.g. plasma concentration of the drug). An example of an immediate effect PKPD model is the direct response PKPD model.
However, more than often, drugs tend to exhibit a time delay between drug concentrations and effect. The delay between time of maximum concentration and time of maximum effect may be caused by various factors, such as a delay in distribution of the drug to its action site or the biological process that the drug affects has its own time course which overall lead to its pharmacological effects. In this setting a delayed effect PKPD model is often used to link a drug’s pharmacokinetics and pharmacodynamics. Examples of delayed PKPD models include the effect compartment (biophase) model which assumes the addition of a hypothetical compartment in which the drug is assumed to exhibit its effects and, the turnover PKPD model which assumes the drug directly influences physiological processes such as the production of an intermediate, hence resulting in the apparent delayed effect.
An understanding of a drug’s pharmacokinetic and pharmacodynamic characteristics are fundamental in ensuring the right medication is prescribed at the right dose and right time for the right patient.